Ojo con esto porque está bastante interesante. Hace aproximadamente 30 años estudiante del grupo indígena Inuit, de Alaska, crearon los números Kaktovik, un sistema numérico con base 20 que es mucho más visual que los números arábigos, por ejemplo.
La buena noticia es que ahora con el apoyo de Silicon Valley, este sistema numérico se incluyó en la actualización de septiembre de 2022 de Unicode. Unicode es un sistema estándar internacional que permite la digitalización de los idiomas escritos en el mundo.

Aún hay mucha chamba que hacer pero ya existe una versión preliminar de fuente para descargar en la computadora y podría aparecer para el sistema operativo Android este mismo año.
Los números Kaktovik
Los inuit son los habitantes nativos del norte de Alaska, Canadá y Groenlandia. Sus comunidades actuales incluyen 34 aldeas en tierras Iñupiaq.
Los números arábigos, que son los que usamos comúnmente, fueron diseñados para un sistema de base 10 por lo que son inadecuados para el iñupiaq y otros idiomas inuit. Y para resolver este problema, los estudiantes de la ciudad de Kaktovik, en Alaska, inventaron en 1994 un sistema numérico de base 20.
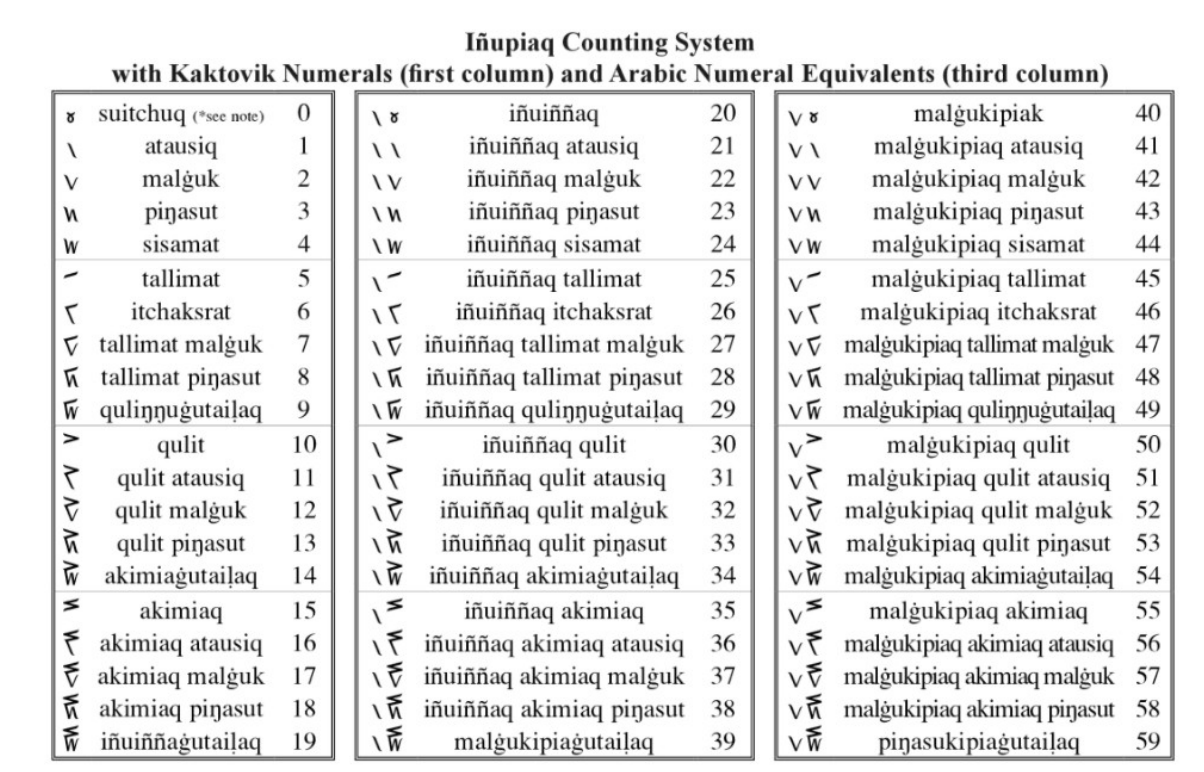
En la siguiente imagen podemos ver la representación icónica de los 19 números de Kaktovik. En este sistema posicional de base 20, el número 20 se escribe con el dígito del 1 seguido del dígito del 0.
Como el idioma no tiene una palabra para el cero, los creadores decidieron que el símbolo para 0 debería verse como unos brazos cruzados, lo que significa que no estaban contando nada.

Lo primero que hay que explicar es que las cantidades se cuenta en puntajes, como en el danés y el galés. Es decir, hay números intermedios para 5, 10 y 15.
Esto sucede porque los números reflejan gráficamente la estructura del idioma. Por ejemplo, el número siete se llama tallimat malġuk en Iñupiaq, es decir, cinco y dos. Si hacemos la suma de esas dos cantidades obtenemos el 7.
Si observamos la imagen anterior, los números del 1 al 4 son similares y solo se va sumando una rayita. Llegando al 5 el patrón cambia y hasta el 9 se van combinando con el primer bloque de símbolos.
El 10, nuevamente, es otro símbolo que se suba con los símbolos anteriores conforme aumenta el número. El 4, por ejemplo, es como una W y el 5 es como un acento. Para obtener el 9 tenemos que sumar 4+9 y el símbolo de 9 lo representa: una W con un acento.

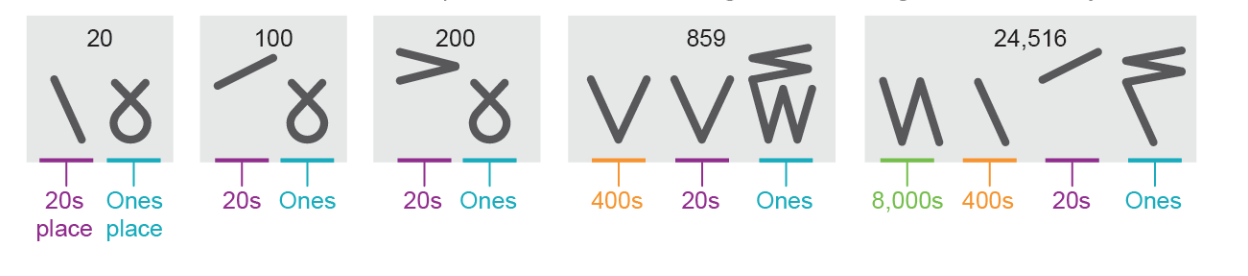
Pero ¿y luego? ¿qué pasa con los siguientes números? Lo primero que tenemos que tener en cuenta es que estamos hablando de un sistema vigesimal, es decir, de 20 en 20 y no de 10 en 10.
Además, este sistema es posicional, como el maya, dependiendo de la posición del símbolo es su valor ya sea 1, 20, 400, 8000 y etc. Vamos a analizar el número 30, por ejemplo…. su símbolo es este:
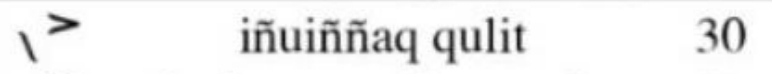
Así a simple vista podemos identificar el símbolo de 1 y de 10, que si lo sumamos pensando en un sistema decimal, tendríamos 11 y no 30.
Pero los números Kaktovik usan un sistema vigesimal. Eso quiere decir que el primer dígito que vemos (a la izquierda) va multiplicado por 20. Es decir, si queremos escribir 30… ocupamos un 20 y un 10 para lograrlo.
El símbolo de 1 es el que se va a multiplicar por 20 para obtener 20 y luego le acompletamos lo que falta con el símbolo de 10: es decir 1 x 20 + 10= 30
Este otro es el símbolo de 50 y aplica lo mismo. El primer dígito tiene que ir multiplicado por 20 siempre. En este observamos el símbolo de 2 al inicio: 2 x 20 nos da 40.
Y ya solo nos falta agregarle un 10 para obtener 50. La idea es pensar en 20 como la unidad principal: 20×1 es 20, 20×2 es 40, 20×3 es 60, 20×4 es 80 y 20×5 es 100. Por eso este sistema es vigesimal con una subdivisión de 5.
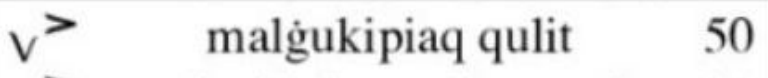
Podemos pensar entonces en una fórmula más o menos así: X(20) + Y=Z.
Para saber cómo escribir un número, después del 19, primero hay que poner en Z el número que queremos escribir. Si queremos el 45, entonces tenemos X(20) + Y =45.
Tons pensamos en un múltiplo de 20 que quede bien, que sería el 2: 20 x 2 son 40. Ya vamos en que 2(20) + Y= 45.
Y ya para acabar le damos a Y el valor que falta para completar la cuenta, es decir, 5. En este sistema el 45 se representa con el símbolo de 2 y el de 5.
¿Y cómo van a llegar estos números Kaktovik a las computadoras y celulares?
En los siglos XIX y XX las escuelas de Estados Unidos prohibieron el idioma de forma violenta. En la década de 1990 estudiantes de una ciudad iñupiaq desarrollaron una idea para crear un sistema numérico que se adaptara a su idioma.
Es tan funcional para ellos que rápidamente se propagó y se comenzó a utilizar las comunidades. Con sanciones y jalones de orejas las escuelas empezaron a aceptar este sistema numérico y el idioma, pero aún es un asunto muy marginal.
Lingüistas de la Universidad de California comenzaron a reavivar los números de Kaktovik y después de mucha chamba los números se incluyeron en la actualización de septiembre de 2022 de Unicode.
Unicode es un estándar de codificación de caracteres diseñado para facilitar el tratamiento informático, transmisión, y visualización de textos de numerosos idiomas y disciplinas técnicas, además de textos clásicos de lenguas muertas.

Un artículo de Scientific American explica que la nueva versión, Unicode 15.0, ofrece un identificador virtual para cada número y esto permite que los desarrolladores los puedan llevar a las pantallas digitales.
Google por su parte ya está creando una fuente para los números basa en esta actualización. Se sabe que hay una versión preliminar que se puede descargar en las computadoras y a finales de verano existirá para el sistema operativo Android.
Eso sí, será necesario también crear teclas de teclado y celulares con estos números para que funcione. Como sea es un avance importantísimo.



